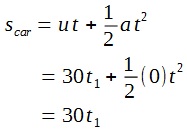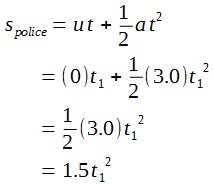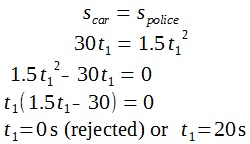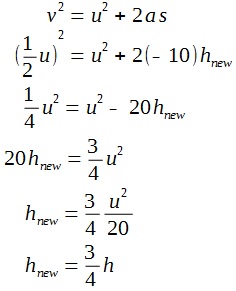Kinematics

James 27 Feb 2017 - 2

Question

A car travelling at a constant speed of 30 ms-1 passes a police car, which is at rest.

The police officer accelerates at a constant rate of 3.0 ms-2 and maintains this rate of acceleration until he pulls next to the speeding car. Assume that the police car starts to move at the moment the car moves past the police car.

What is the time required for the police officer to catch up with the car?

Answer

We assume that the police car catches up with the car at time t1.

The following formula for displacement can be obtained:

When the police car catches up with the car, both have travelled the same displacement.

The police car requires 20 s to catch up with the car.

James 27 Feb 2017 - 1

Question

A body is thrown vertically up from the ground with an initial speed u and it reaches the maximum height h at time t0.

What is the height it reaches at ½ t0?

Answer

We first define the upwards direction as positive.

When the body reaches the maximum height, the speed of the body is 0.

Knowing this, we can find expressions for h and t0. The acceleration of the body is taken to be 10 ms-2 downwards. Since we define upwards to be positive, the acceleleration will be -10 ms-2.

When the time is ½ t0,

Now that we know the speed at ½ t0, we can find the height travelled by the body.

James 25 Feb 2017

Question

A student flips a coin into the air. Its initial velocity is 8.0 ms-1. Taking g = 10 ms-2 and ignoring air resistance, calculate:

a) the maximum height, h, the coin reaches, [2]
b) the velocity of the coin on returning to his hand, [1]
c) the time that the coin is in the air. [2]

Answer

a) To easily solve the problem, the velocity-time graph has to sketched.

Since there is no air resistance, the acceleration will be constant at 10ms-2 downwards. This means that the graph is a straight line.

At the highest point, the velocity of the coin will be zero.

The maximum height is given by the shaded area below.

To find the area we first need to find the value of th. Since we are taking upwards to be positive, the acceleration is -10 ms-2.

b) Since the coin falls back down to the student, the distance travelled downwards must be equal to the distance travelled upwards.

This means that the two shaded areas must be the same.

By symmetry, the final velocity of the coin must be -8.0 ms-1.

c) Since the area of the shaded areas are the same, the time taken for the upward journey and the downward journey must also be the same.

Hence the total time taken is twice the time taken for the coin to reach the highest point.

David 07 May 2016 - 4

Question

A stone is thrown vertically upwards with a velocity of 5.0 m/s. After time t, it reaches the original position. Neglecting air resistance, what is the time required for the ball to reach the highest position?

Answer

By conservation of energy, the final velocity of the stone will be 5.0 m/s downwards. We also know that the acceleration of the stone is constant at 10m/s2 downwards. Hence, we can sketch a velocity-time graph.

The displacement upwards from 0 to 0.5 t must be equal to the displacement downwards from 0.5 t to t since the stone returns to its original position.

By symmetry, the highest point must be at 0.5 t.

Hence, the ball takes 0.5t to reach the highest point.