Question
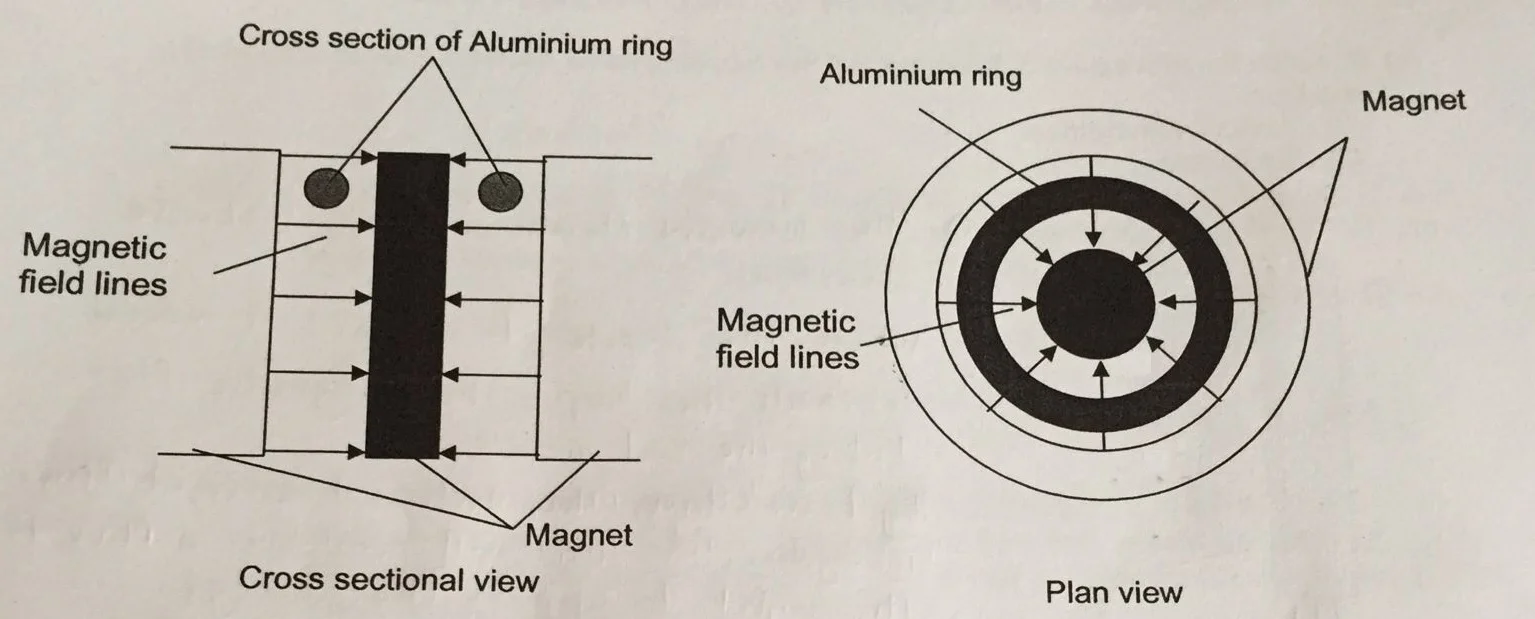
The figure below shows the cross section of a long cylindrical magnet, as well as the plan view of the radial magnetic field. The cylindrical magnets are placed vertically. A thin circular aluminum ring of radius r and resistance R falls through the magnetic field as shown in the diagram. In the vicinity of the aluminum ring, themagnetic flux density is 2.0 T.
[Resistivity of aluminium = 3.1 x 10-8 Ω m, density of aluminium = 2.7 x 103 kg m-3]
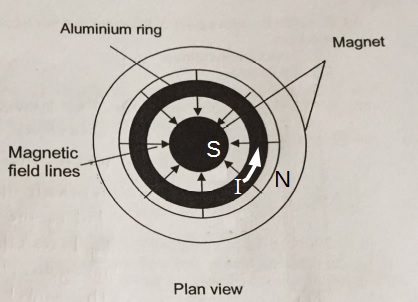
a) By considering the plan view of the magnet, indicate the polarity of the magnets and the direction of the induced current.
b) Describe the motion of the aluminum ring when it is released in the radial magnetic field.
c) Show that the current in the aluminum ring when it is falling at a speed v is given by
\( I= {{2 \pi r B v} \over {R}}\)
d) Calculate the terminal velocity of the ring.
Answer
a) Magnetic field lines are from the North pole to the South pole, hence the outer ring is a North pole and the inner cylinder is a South pole.
Based on Fleming's Right hand rule, since the ring is moving into the page and the magnetic field lines are radially inwards, the induced current flows in the anti-clockwise direction.
b) When it is first released, it falls with an acceleration of 9.81 ms-2. As velocity of the the aluminium ring increases, the acceleration of the ring decreases until it eventually reaches zero. The ring has reached terminal velocity.
c)
d)