Minqi 19 May 2016 - 4

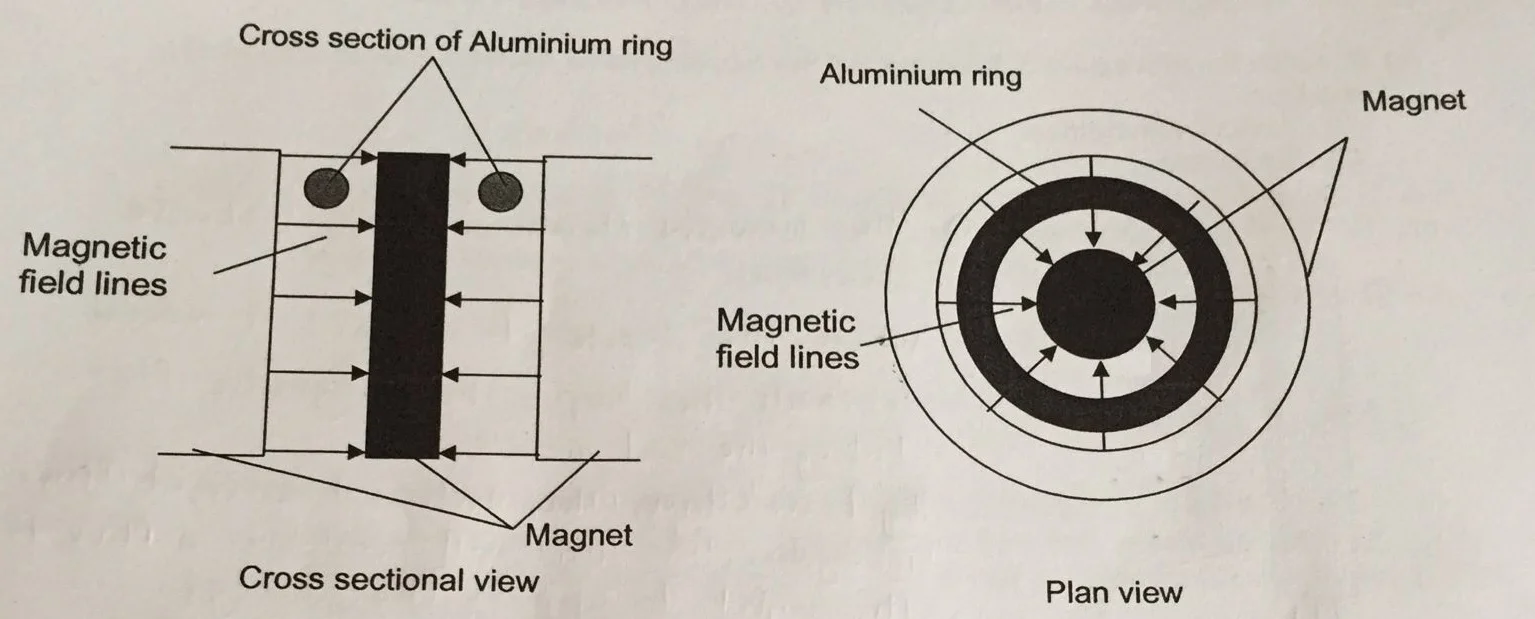
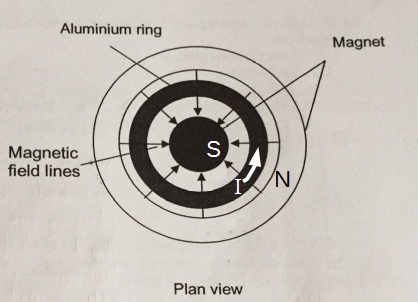
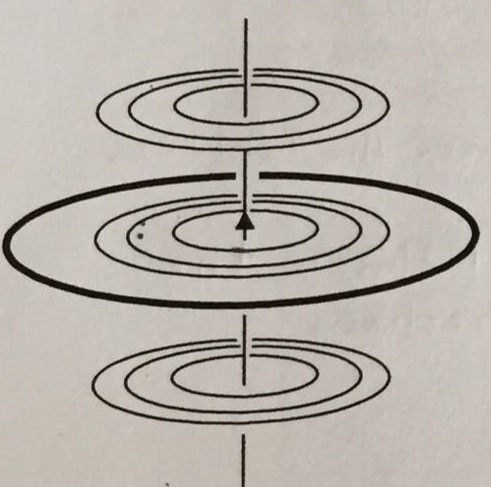
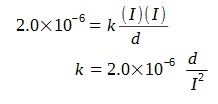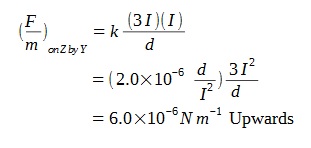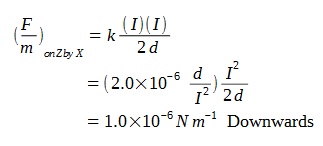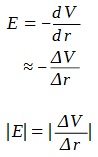Question

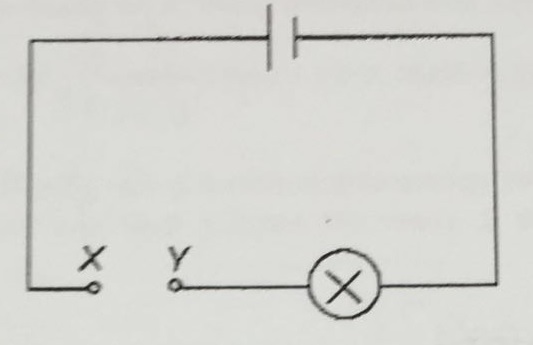
A set-up to control the brightness of a bulb is shown below.

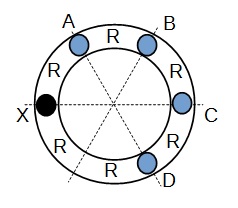
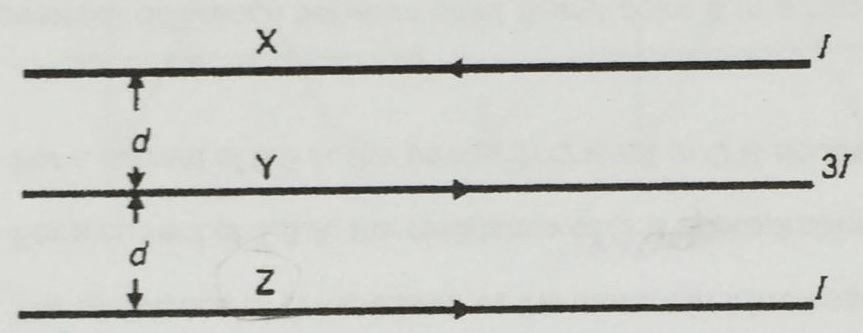
X and Y are to connected to a uniform circular ring which has a constant cross-sectional area and resistivity X is connected to the left side of the ring.

Where should Y be connected for the light to be the dimmest?

---

Answer

The circular ring and its connection point can be seen as a connection of 6 resistors of resistance R as shown below:

When Y is connected to A, the connection is as shown below:

The effective resistance is 0.833 R.

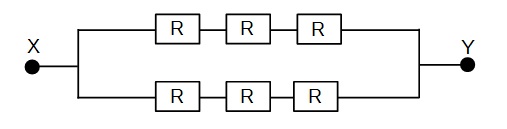
When Y is connected to B, the connection is as shown below:

The effective resistance is 1.33 R.

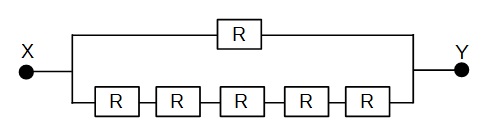
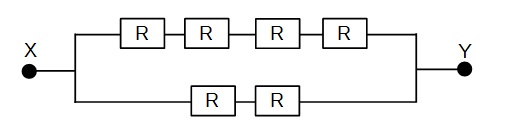
When Y is connected to C, the connection is as shown below:

The effective resistance is 1.5 R.

When Y is connected to D, the connection is as shown below:

The effective resistance is 1.33 R.

Hence, connecting Y to C will result in the greatest resistance and the light bulb will be the dimmest.

Minqi 19 May 2016 - 3

Question

The diagram below shows three parallel wires X, Y and Z placed in a horizontal plane. Wires X and Z carry current I in opposite directions. Wire Y carries a current of 3I in the direction shown and is equidistant from the other wires.

The magnitude of the force per unit length between two parallel wires placed a distance apart, each carrying a current of I is 2.0 x 10-6 N m-1. What is the direction and magnitude of the net force per unit length acting on the wire Z?

(The force per unit length is proportional to the product of the currents in the two wires and inversely proportional to the separation between them.)

---

Answer

Based on the information regarding the forces per unit length between two wires,

\( {F \over m} = k {I_1 I_2 \over r} \)

Based on the value of the force given,

The force between Y and Z is attractive because the currents in both wires are flowing in the same direction.

The force between X and Z is repulsive because the currents in both wires are flowing in the opposite directions.

Hence, the resultant force per unit length is 5.0 x 10^-6 N m^-1 upwards towards Y.

Minqi 19 May 2016 - 2

Question

The figure shows a full scale diagram of equipotential lines of an electric field, with potential difference of 3.0 V between adjacent lines.

What is the closest estimate of the magnitude and direction of the field strength at P along the dotted line?

---

Answer

The electric field lines are from the positive charge to the negative charge, hence, the direction of the electric field strength is towards the left.

To calculate the electric field strength, we use the following relationship:

Since the diagram is drawn full-scale, we need to measure the distance d as shown in the diagram below using a ruler.

The potential difference between the 2 lines are 6.0 V.

Hence the electric field strength is \( \left | E \right | = \left | 6.0 \over d \right | \) towards the left.

Minqi 19 May 2016 - 1

Question

A beam of initially unpolarised light passes through three polaroids P, Q and R. Polaroid P's axis of polarisation is vertical. Which orientation of polaroids Q and R with respect to the vertical axis will produce an emergent beam from polaroid R with maximum intensity.

Orientation with respect
to the vertical axis

         Q         R
A     45^o      45^o
B     45^o      90^o
C     90^o      180^o
D     180^o     60^o

---

Answer

When a wave polarised in one axis passes through another polaroid with the axis at an angle of θ, only the component of the wave parallel to the new axis can pass through.

A₁ = A₀ cos θ

After passing through the second polaroid placed at an angle of ϕ, the final amplitude will be given by

A₂ = A₁ cos ϕ

Hence, the final intensity will be given by

A₂ = A₁ cos ϕ
= ( A₀ cos θ ) cos ϕ

I₂ = k ( A ₂ )²
= k ( A₀ cos θ cos ϕ )²
= k A₀² cos² θ cos² ϕ
= I₀ cos² θ cos² ϕ

For option A,
I₂ = I₀ cos² θ cos² ϕ
= I ₀ cos² 45 ^o cos² (45^o - 45 ^o)
= 0.50 I₀

For option B,
I₂ = I ₀ cos² θ cos² ϕ
= I₀ cos² 45^o cos² (90^o - 45^o)
= 0.25 I₀

For option C,
I₂ = I₀ cos² θ cos² ϕ
= I₀ cos ² 90^o cos² (180^o - 90^o)
= 0

For option D,
I₂ = I₀ cos² θ cos²ϕ
= I₀ cos²180^o cos²(180^o - 60^o)
= 0.25 I₀

Hence, Option A will produce a beam with maximum intensity.

Minqi 02 Apr 2016 - 2

Question

The figure below shows the cross section of a long cylindrical magnet, as well as the plan view of the radial magnetic field. The cylindrical magnets are placed vertically. A thin circular aluminum ring of radius r and resistance R falls through the magnetic field as shown in the diagram. In the vicinity of the aluminum ring, themagnetic flux density is 2.0 T.

[Resistivity of aluminium = 3.1 x 10^-8 Ω m, density of aluminium = 2.7 x 10³ kg m^-3]

a) By considering the plan view of the magnet, indicate the polarity of the magnets and the direction of the induced current.

b) Describe the motion of the aluminum ring when it is released in the radial magnetic field.

c) Show that the current in the aluminum ring when it is falling at a speed v is given by

\( I= {{2 \pi r B v} \over {R}}\)

d) Calculate the terminal velocity of the ring.

---

Answer

a) Magnetic field lines are from the North pole to the South pole, hence the outer ring is a North pole and the inner cylinder is a South pole.

Based on Fleming's Right hand rule, since the ring is moving into the page and the magnetic field lines are radially inwards, the induced current flows in the anti-clockwise direction.

b) When it is first released, it falls with an acceleration of 9.81 ms^-2. As velocity of the the aluminium ring increases, the acceleration of the ring decreases until it eventually reaches zero. The ring has reached terminal velocity.

c)

d)

View fullsize

Minqi 02 Apr 2016 - 1

Question

A long, straight wire, which carries a current, is placed in the vicinity of a circular coil. Using the definition of magnetic flux, explain the following statements.

a) When the wire is placed along the diameter of the coil, the net flux through the coil is zero.

b) When the wire is placed along the axis to the coil, the net flux through the coil is zero.

---

Answer

a) The perpendicular component of the magnetic flux density with respect to the area of the coil on the left side of the coil is into the page.

The perpendicular component of the magnetic flux density with respect to the area of the coil on the right side of the coil is out of the page.

By symmetry, the magnitude of the magnetic flux density on both sides are the same.

Hence, the resultant perpendicular component of the magnetic flux density is zero. Therefore, the magnetic flux through the coil is zero.

b) The magnetic field lines are along the surface of the coil. This means that the perpendicular component of the magnetic flux density with respect to the area of the coil is zero.

Hence, the magnetic flux through the coil is zero.

Minqi 11 Feb 2016

Question

Two charged sole metal spheres A and B are situated in a vacuum. Their centres separated by a distance of 12.0 cm as illustrated in Fig. 2.1. The diagram is not to scale.

Point P is a point on the line joining the centres of the two spheres. Point P is a distance x from the centre of sphere A.

The variation with distance X of the electric field strength E at point P is shown in Fig 2.2. A positive value of E on the graph at a point corresponds to an electric field vector pointing horizontally to the right.

State and explain:

1. the signs of charges of A and B.

2. the ratio of the radius of sphere A to that of sphere B.

3. how the electric potential varies inside spheres A and B.

---

Answer

1. Both A and B are positive.

Near A, the electric field strength is positive. This means that the electric field strength is in the direction towards the right and away from A. This means that a positive point test charge will experience a force away from A. Hence A is positive.

Near B, the electric field strength negative. This means that the electric field strength is in the direction towards the left and away from B. This means that a positive point test charge will experience a force away from B. Hence B is positive.

2. From the graph, we can see that the radius of A given by the region from x = 0.0 cm to x = 1.4 cm where the electric field strength is zero. Hence, the radius of sphere A is 1.4 cm.

The radius of sphere B is given by the the region from x = 11.4 cm to x = 12.0 cm where the electric field strength is zero. Hence, the radius of sphere B is 0.6 cm.

Therefore, the ratio is 7 : 3.

3. The electric potential remains constant inside sphere A and sphere B. This is because the of the relationship \(E = -{dV \over dx}\). Since E is 0 inside the spheres, V must be constant in order for \( {{dV} \over {dx}} \) to be 0.

(Since the spheres are conductors, the electric charges in the form of mobile electrons inside are free to move. If there is a potential difference, there will be an electric force on the electrons. These electrons will move and redistribute themselves until there is a constant electric potential inside the sphere and no longer any electric force on the electrons.)