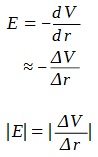Electric Fields

Jia Yee 25 Aug 2016

Question

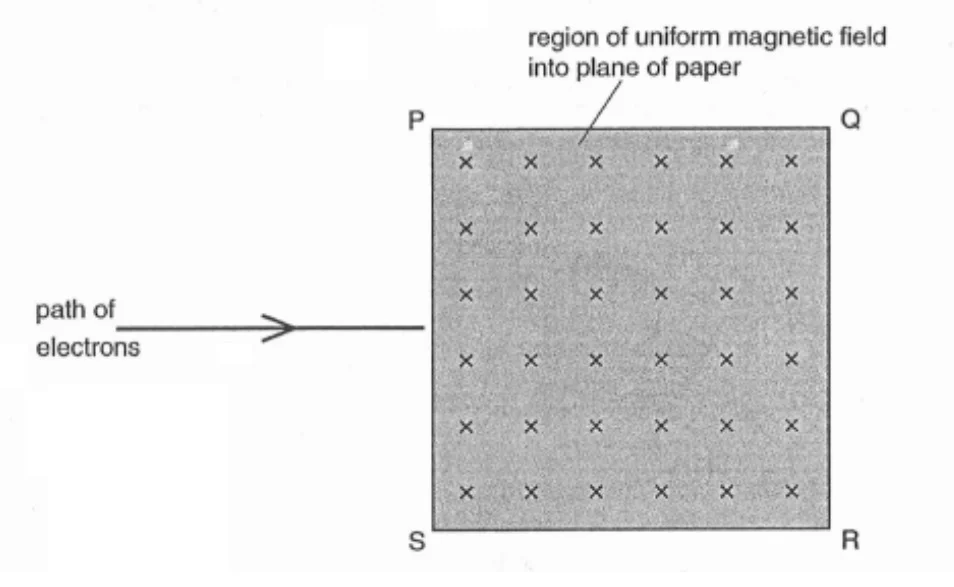
The figure below shows a region PQRS of a uniform magnetic field directed downwards into the plane of the paper.

Electrons, all having the same speed, enter the region of the magnetic field.

a) On the figure, show the path of the electrons as they pass through the magnetic field emerging from side QR.

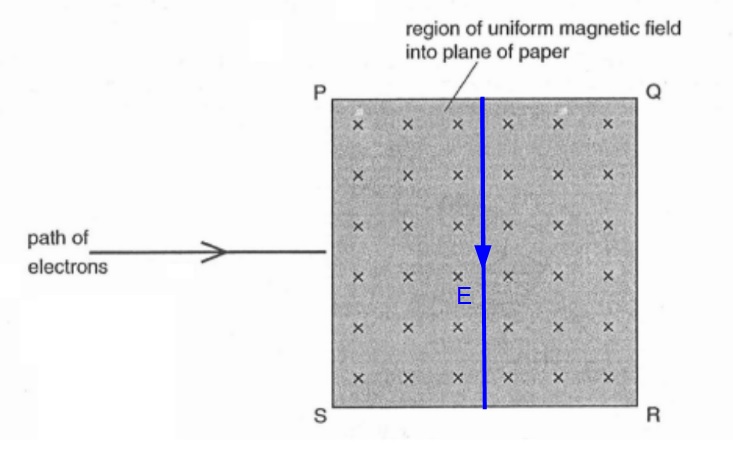
b) A uniform electric field is also applied in the region PQRS so that the electrons now pass undeflected through this region. On the figure, mark with an arrow labelled E, the direction of the electric field.

c) The undeflected electrons in (b) each have charge -e, mass m and speed v. State and explain the effect if any, on the particles entering the region PQRS of the same magnetic and electric fields in (b) if the particles each have

i) charge -e, mass m and speed 2v.

ii) charge +e, mass m and speed v.

Answer

a) Since the electrons are moving to the right, it is the same as a current flowing to the left. By using Flemming’s left hand rule, the magnetic force on the electrons is downwards.

According to Flemming’s left hand rule, the magnetic force will always be perpendicular to the velocity of the electrons. This means that it provides a centripetal force. Hence, the electrons will move in a circular path as shown.

Once the electrons exit the magnetic field, they will move in a straight path since there is no resultant force acting on the electrons. We ignore the effects of the weight because the acceleration of due to the weight is too small to cause any significant change in the velocity of the electrons.

b) In order for the electrons to pass through undeflected, the resultant force on the electrons must be zero. Since the magnetic force on the electrons is downwards, the electric force acting on the electrons must be of the same magnitude and acting upwards.

In order for the electric force to be acting upwards, electric field lines must be directed downwards. (Since electrons are negatively-charged, they will experience an electric force in the opposite direction to the electric field lines.)

c)  When an electron is moving with a speed of v, it passes straight through without any deflection. The magnetic force and electric forces on the electrons are given by the following formulae:

FB= Bqv
FE = qE

Since the downwards magnetic force is now greater than the upwards electric force, the resultant force is downwards and the particle will curve downwards as it passes through the region.

ii) When a particle of the opposite charge (+e) and mass (m) and same speed (2v) moves through the field, the directions of the magnetic force and electric forces are now reversed.

The electric force acts downwards and the magnetic force acts upwards on the particle.

However, both forces are still of the same magnitude and the resultant force is still zero. Hence, the particle will still pass through the region undeflected.

Minqi 19 May 2016 - 2

Question

The figure shows a full scale diagram of equipotential lines of an electric field, with potential difference of 3.0 V between adjacent lines.

What is the closest estimate of the magnitude and direction of the field strength at P along the dotted line?

Answer

The electric field lines are from the positive charge to the negative charge, hence, the direction of the electric field strength is towards the left.

To calculate the electric field strength, we use the following relationship:

Since the diagram is drawn full-scale, we need to measure the distance d as shown in the diagram below using a ruler.

The potential difference between the 2 lines are 6.0 V.

Hence the electric field strength is \( \left | E \right | = \left | 6.0 \over d \right | \) towards the left.

Minqi 11 Feb 2016

Question

Two charged sole metal spheres A and B are situated in a vacuum. Their centres separated by a distance of 12.0 cm as illustrated in Fig. 2.1. The diagram is not to scale.

Point P is a point on the line joining the centres of the two spheres. Point P is a distance x from the centre of sphere A.

The variation with distance X of the electric field strength E at point P is shown in Fig 2.2. A positive value of E on the graph at a point corresponds to an electric field vector pointing horizontally to the right.

State and explain:

1. the signs of charges of A and B.

2. the ratio of the radius of sphere A to that of sphere B.

3. how the electric potential varies inside spheres A and B.

Answer

1. Both A and B are positive.

Near A, the electric field strength is positive. This means that the electric field strength is in the direction towards the right and away from A. This means that a positive point test charge will experience a force away from A. Hence A is positive.

Near B, the electric field strength negative. This means that the electric field strength is in the direction towards the left and away from B. This means that a positive point test charge will experience a force away from B. Hence B is positive.

2. From the graph, we can see that the radius of A given by the region from x = 0.0 cm to x = 1.4 cm where the electric field strength is zero. Hence, the radius of sphere A is 1.4 cm.

The radius of sphere B is given by the the region from x = 11.4 cm to x = 12.0 cm where the electric field strength is zero. Hence, the radius of sphere B is 0.6 cm.

Therefore, the ratio is 7 : 3.

3. The electric potential remains constant inside sphere A and sphere B. This is because the of the relationship \(E = -{dV \over dx}\). Since E is 0 inside the spheres, V must be constant in order for \( {{dV} \over {dx}} \) to be 0.

(Since the spheres are conductors, the electric charges in the form of mobile electrons inside are free to move. If there is a potential difference, there will be an electric force on the electrons. These electrons will move and redistribute themselves until there is a constant electric potential inside the sphere and no longer any electric force on the electrons.)